Chap 3. 게이트 레벨 최소화 (4) . Gate-Level Minimization
3-8. 2레벨 구현 (two-level implementation)
이렇게 범용적인 만능 NAND 게이트로 2-레벨 부울 함수를 구현하기 위해서는 먼저 부울 함수를 곱의 합(sum of products) 형식으로 표현해야 한다.
언제나 그랬듯. 예시를 들어보자.

부울함수 F에서. AND와 OR을 써서 우리가 평소 구현하듯이 구현하면.
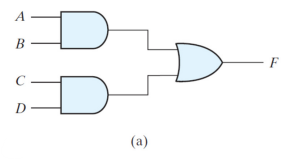
여기서 모든 게이트를 NAND로 구현하기 위해선. 앞서 배운 NAND의 기호를 이용하듯이 하면 된다. (bubble 이용)

AND 앞에 bubble을 붙여 NAND를 만들고. 붙여진 라인과 맞닿은 게이트에도 똑같이 bubble을 붙여줘 NOR을 만든다.
따라서 앞서 배운 NAND의 두가지 표현이 같이 있는 (AND게이트와 OR게이트에 bubble이 붙여진 형태) 회로가 된다.

게이트 심볼은 bubble의 위치가 바뀔 때 같이 바뀐다. (AND ↔ OR)
이를 이용해 NAND gate만이 살아남은 2레벨 구현회로를 만들어낸다.
이를 예제에 적용해 보자면.

1. 첫 단계는 함수를 곱의 합(sum of products) 형식으로 간략화하는 것이다.
간략화 방식은 우리가 배운 방법인 K-map 방식을 이용한다. (F = xy' + x'y +z)
2. 그 이후 AND와 OR, NOT을 이용하여 논리회로를 설계한다.
3. NAND gate 구현회로로 나타내기 위해 bubble을 이용하여 Mixed notation 회로까지 구현한다.
4. 최종적으로 bubble의 위치를 옮겨(NAND gate가 생기도록) 최종 NAND gate implementation을 완성한다.
(예제에서 한 것 처럼 입력단은 bubble을 붙이는 작업을 하지 않고 입력 자체를 보수화해서 표현할 수 있다)
3-9. 다중레벨 NAND 회로 (Multilevel NAND sircuits)
부울 함수를 표준 형식(standard form)으로 표현하면 결국 2-레벨 회로로 구현된다.
그러나 디지털 시스템은 3-레벨 혹은 그 이상 레벨의 게이트 구조로 설계되는 경우도 있다.
다중레벨 회로 설꼐의 가장 일반적인 과정은 AND OR NOT 의 연산으로만 표현하는 것이다.
그 다음 함수를 NAND gate 회로로 변환할 수 까지 있게 되었다.

위와 같은 부울 함수 F가 있을 때. 부울 연산의 순서대로 괄호에서 AND,OR 연산까지 설계를 한다면 (a)와 같다.
(식 그대로의 논리회로 설계)
또한 위에서 배운것과 같이 NAND gate를 가지는 회로로 구현하기 위해 bubble을 붙여 이용하면 (b)와 같다.
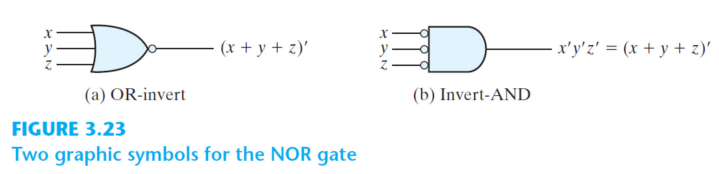
3-9. NOR 구현 (NOR implementation)
NAND와 같이 NOR gate도 범용 게이트이다. (universal gate)
다시 말하자면 NAND와 같이 NOR 만 이용해서 논리회로를 구현할 수 있다는 것이다.
이러한 성질은 NOR 연산은 부울 함수에서 NAND 연산과 쌍대(dual) 관계이기 때문이다.
아래의 그림은 NOR gate 를 이용해 NOT, OR, AND 의 연산을 만들어내는 과정을 보여준다.

NAND 와 마찬가지로 NOT 의 구현은 NOR을 한가지 인풋으로 고정시켜 단일 입력 NOR로써 만들어준다.