Chap 2. 부울 대수와 논리 게이트 (2) . Boolean Algebra and Logic Gates
2-4. Canonical(정준형식) and Standard(표준형식) Forms.
1. 정준형식 Canonical Form

먼저 2진 변수는 x와 같은 정상적 형식과 또는 x'과 같은 보수의 형식으로 표시할 수 있다.
AND 연산으로 결합된 2개의 2진 변수 x와 y를 생각해 볼 때. 각 변수는 둘중 한 형식으로 나타날 것이므로 네 가지 조합이 가능하다. ( x'y', x'y, xy', xy)
이들 4개 AND형식을 최소항 (minterm) 또는 표준곱 (standard product)이라고 한다.
위의 표에서 왼쪽 minterms 부분부터 본다면. 각 x y z에 대한 한 변수 조합에서 하나의 minterm이 생성된다.
-최소항 minterm 생성 규칙-
1. 0은 보수의 형태, 1은 정상적 형태로 표기한다
2. 각 변수에 대한 한가지 조합에 하나의 minterm이 생성된다.
3. minterm은 각 변수의 AND 형식의 결합으로 이루어진다.
4. 각 변수에 대한 minterm은 항상 결과가 1이 되도록 생성한다.
→ 최소항은 AND로 가능한 조합의 보수형태.
같은 방식으로 OR의 항에서 발생하는 가짓수를 최대항 (maxterm) 또는 표준합 (standard sum) 이라고 표현한다.
-최대항 maxterm 생성 규칙-
1. 0은 정상적 형태, 1은 보수의 형태로 표기한다.
2. 각 변수에 대한 한가지 조합에 하나의 maxterm이 생성된다.
3. maxterm은 각 변수의 OR 형식의 결합으로 이루어진다.
5. 각 변수에 대한 maxterm은 항상 결과가 0이 되도록 생성한다.
→ 최대항은 OR로 가능한 조합의 보수형태.

이렇게 구해진 최소항과 최대항으로. 어떠한 부울 함수식도 구해낼 수 있다.
(어떠한 부울 함수이던지 최소항과 최대항으로 표현할 수 있다.)
→ 최소항 자체가 결과값이 하나라도 들어올 때 1로 나오도록 만들어진 AND결합이다, 최소항의 OR 결합의 표기는 결국 결과값이 0인 항은 0으로 출력되고, 나머지 항에서 결과를 1로 만드는 최소항의 입력이 들어온다면 그 최소항만 1로 켜지기 때문에 부울 함수를 구해낼 수 있다.
진리표를 보고 부울 함수로 구해낼 수 있는 방법은.
각 변수 조합의 값이 1인 항들을 더하여 (OR연산) 최소항 부울 식을 구한다. (F1, F2)
이는 우리가 구해낸 부울함수가 최소항으로만 이루어져 있으므로, 결과값이 0으로 나오는 변수조합이 들어오면 모든 부울 함수의 항이 0으로, 결과값이 1로 발생하는 조합이 들어오면 해당하는 최소항만 1로 들어옴 (나머지는 무조건 0)

최대항을 이용하여 부울함수를 구해내는 과정은 최소항의 정확히 반대 과정이다.
각 변수의 조합이 결과를 0으로 출력하는 최대항들만 뽑아서 AND 결합으로 표기한다.

결과적으로 정준형식 (canonical form)에는 최소항들의 덧셈 (sum of minterms) 혹은 최대항의 곱 (product of maxterms)으로 표기되는 형식을 말한다. (서로 같은 함수를 나타내지만 최소항/최대항으로 다르게 표현가능)
2. 표준형식 Standard Form
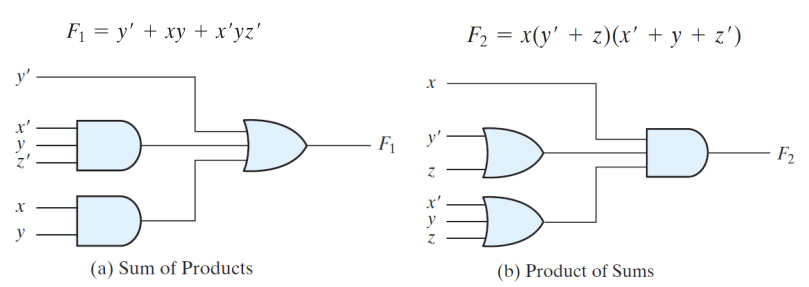
부울 대수는 두 가지 정준 형식이 있다. 한 형식은 위에서 보았던 것과 같이 진리표로부터 함수를 읽어서 얻은 기본 형식이다. 그러나 이 형식에서는 각 최소항이나 최대항들이 모든 변수를 포함하기 때문에 우리가 원하는 최소한의 수를 가진 리터럴을 뽑아낸 형식으로는 볼 수 없다.
표현할 수 있는 다른 방법은 바로 '표준 형식 standard form'이다. 여기서는 항은 1개, 2개 또는 임의의 수의 리터럴을 가질 수 있다. 이 표준 형식에서는 곱의 합 (sum of products) 혹은 합의 곱 (product of sums)으로 나타낼 수 있다.
이는 최소항 혹은 최대항을 사용하지 않고 곱의 합이나 합의 곱을 이용하여 표현한다는 것이다.
이렇게 표현된 위의 회로를 Two-level implementation (2-레벨 구현) 이라고 부른다.

당연하게도, 표준형태로 이루어지지 않는 회로도 존재한다. 그러나 곱의 합도, 합의 곱도 아닌 이 식을 표준형식으로 표현할 수 있다. 위의 함수를 표준 형식으로 표현하려면 분배 법칙을 사용하여 괄호를 없애야 한다. (괄호가 하나의 연산을 대표해 하나의 level이 더 생기기 때문)