들어가며.
게이트 레벨 최소화(gate-level minimization)은 앞서 배운 부울 대수를 이용한 논리회로 설계에서 지향하고 있는 목표점이라고 보면 된다.
말을 내가 어렵게 해서 그런데, 그냥 가장 최소화(minimization) 된 회로를 구하는 최종 목표를 이루는 방법중 하나를 배울 것이라고 생각하면 된다.
그 중에서도 우리는 카르노 맵 방법 (The map method / Karnaough map / K-map method)을 통해 구해낼 것이다.
당연히 이 방법을 모르고 앞서 배운 부울대수의 공준과 정리를 이용해서 정리할 수 있다. 하지만 그 개별적인 계산은 조금만 복잡한 회로가 주어지면 금세 풀 수 없을 정도로 복잡해진다(...)
K-map 방식은 네모 칸들로 구성된 다이어그램이고, 각 네모 칸은 최소화하고자 하는 함수의 최소항들이 들어간다. 임의의 부울 함수는 최소항의 합으로 표시할 수 있으므로(Canonical form/정준형식) 함수에 포함된 최소항들은 그 최소항에 해당하는 네모칸에 시각적으로 표현할 수 있게된다.
이렇게 맵에 의해 간략화된 표현은 항상 곱의 합 또는 합의 곱이라는 두 표현(Standard form/표준형식)중 하나가 된다.
가장 간략화된 대수적 표현식은 항의 개수가 최소이고, 각각의 항이 가장 적은 수의 리터럴(literal)을 갖는 식을 의미하게 된다. 이러한 표현식은 가장 적은 수의 게이트와 게이트 당 가장 적은 수의 입력을 갖는 회로도를 생성하게 된다. (부울 함수에 의한 회로도의 표현)
-K-map 활용 방법, 순서-
1. 진리표나 정준형식으로 주어진 함수를 K-map화 한다.
2. 인접한 1을 묶고, 각 묶음에서 변하지 않는 변수의 항을 구한다.
3. 2^n 개씩 묶어야 하며(짝수개로), 이 때 각 묶음은 총 변수 개수에서 n을 뺀 변수로 표현된다. 한번 사용된 1을 여러번 묶을 수도 있다.
4. 각 묶음을 나타내는 항을 더해서 sum of products의 함수로 적는다.
5. 단순화된 함수록 logic-gate implementation 한다.
역시나 백문이불여일견 이라고, 각 변수에 맞는 방법을 따라가다 보면 위의 난잡해보이는 말들이 자연스럽게 이해된다.
3-1. 2변수 K-map
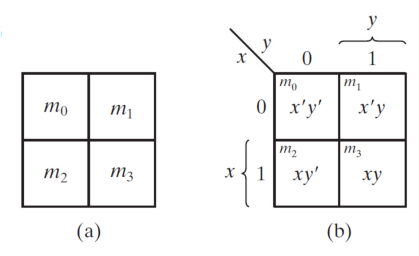
K-map을 그릴때는 기본적으로 K-map에서 약속된 칸과 순서를 따른다.
(a)의 그림과 같이. 우리가 최소화하고자 하는 2변수 부울 함수 혹은 진리표가 제시되어 있다면.
(진리표가 제시되어 있다면 부울함수 필요 x, 부울함수만 있다면 2변수에 겅우의 수를 넣으며 진리표 생성)
주어진 함수에 속하는 최소항의 결과가 정해진 네모 칸 안에 표시된다.

함수의 값이 1이 되는 부분의 변수조합에서 나온 최소항의 칸만 1을 쓰고 나머지는 비워둔다 (어짜피 0이기 떄문)

현재 2변수 k-map에서, 최대로 묶을 수 있는 2^n의 경우는 4개이다. 그러나 4개를 묶을 수 있는 방법은 없다.
그 다음 묶을 수 있는 경우는 2개씩이다. 현재 k-map위에 써있는 1들을 활용해 모두 한번씩은 묶이도록 묶는다.
이 때 묶여진 묶음마다. 그 묶음 안에서 변하는 변수와 변하지 않는 변수를 파악한다.
위의 예시에서 첫번째 묶음을 가로 묶음이라고 봤을 때. x는 변하지 않고 y만 변화한다.
두번째 묶음을 세로 묶음이라고 봤을 때. x는 변하고 y는 변하지 않는다.
이 때 변하지 않는 항을 그대로 쓴다. (변하는 변수는 버린다.)
이 때 변하지 않는 항은 최소항의 형태로 써야 한다 (y'이였으면 그대로 y'으로 써야한다.)
결론적으로 예시에서 첫번째 묶음은 x, 두번째 묶음은 y의 결과가 나타난다.
결과로 나온 변수를 OR으로 결합한다.
이러한 결과는 canonical form의 형태에서 가장 단순화된 simplified form의 결과이다.
이렇게 카르노맵의 묶음이 항으로 나오는 이유는. 앞에서 배운 정준형식의 분배법칙이 성립하기 때문이다.
ex) xy' + xy = x (y' + y)
= x * 1 (y'과 y의 and는 어떤 값이더라도 1)
=x
→ 묶음으로 사용하면 위의 계산식이 짜여지고 변하는 변수 (위에서는 y'+y)는 1로써 버려지게 된다.
결국 변하지 않는 변수 x만 살아남는다.
또한 한번 묶인 1을 다시 묶음에 사용할 수 있는 이유는 부울대수에서
x + x = x 라는 and의 연산 때문이다.
(우리가 원래 사용하던 대수학에서는 성립 x)
3-2. 3변수 K-map

3변수 k-map의 방법도 동일한데 map 위에 써야하는 최소항의 순서가 다르다.
(이렇게 배치하는 이유는 우리가 2변수에서 봤듯이 변하는 변수를 하나씩 나타나도록 하기 위해 조작한 것이다.)
예를들어 xyz에서 x만 변하거나, y만 변하거나, z만 변하고 나머지는 변하지 않아야. 우리가 묶어서 식을 만들 수 있다.
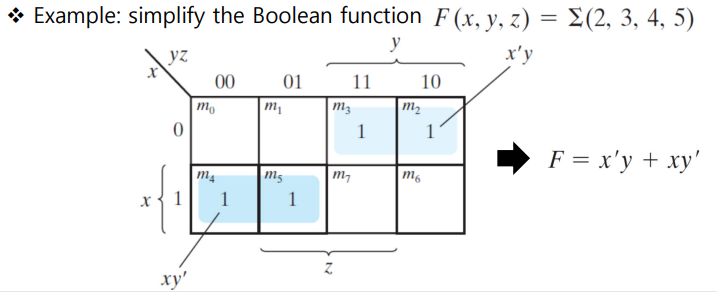
3변수 k-map에서도 각 변수 조합의 결과가 1이 나오는 최소항의 칸에만 1을 써 넣는다.
그 후 2^n (n= 0,1,2,3) 에서 가능한 묶음의 조합을 생각한다. (여기서는 8개 4개 2개)
첫번째로 8개를 모두 묶을 수 있는 인접한 1의 경우는 없다.
두번째로 4개를 모두 묶을 수 있는 인접한 1의 경우는 없다.
세번째로 2개씩 묶을 수 있는 인접한 1은 두개가 존재한다. (첫번째 행 두번째 행)
묶여진 묶음에서 변하는 변수와 변하지 않는 변수를 파악한다.
(첫번째 행의 묶음 : x,y는 변하지 않음, z는 변함. 두번재 행의 묶음 : x,z는 변하지 않음, y는 변함)
이 때 변하는 변수는 버리고, 변하지 않는 변수만 최소항의 값을 가져온다.
※ Adjacent squares 인접한 사각형 개념.
우리는 위의 경우과 같이 특정한 방식을 이용해서 최소항들을 배치시켰기 때문에 '인접한 사각형' 이라는 특이한 성질을 가지게 된다.

그림과 같은 3변수 k-map을 풀어야 할 때. m4 m6위치의 1은 서로 동떨어진 1이라고 보이지만. 상하, 좌우 끝의 칸들은 서로 이어져 있다고 생각할 수 있다. (넘어서 묶어낼 수 있다는 뜻)
따라서 각 하나의 1로 보고 항을 만드는 것이 아니라. m4와 m6을 2개짜리 묶음으로 묶어내서 항을 만들어야 한다.
결국. m4 와 m6을 따로 동떨어진 1이라고 생각해서 구한 xy'z' + xyz' + yz 가 아니라. (그냥 보기에도 simplization 안됨)
m4와 m6을 '인접한 사각형' 성질을 사용해서 묶어내면 yz + xz' 이라는 간소화 식으로 표현된다.
(그냥 식으로 보더라도 우리가 앞에서 본 부울 대수의 공준과 정리로 다시한번 간소화 시킬 수 있다)
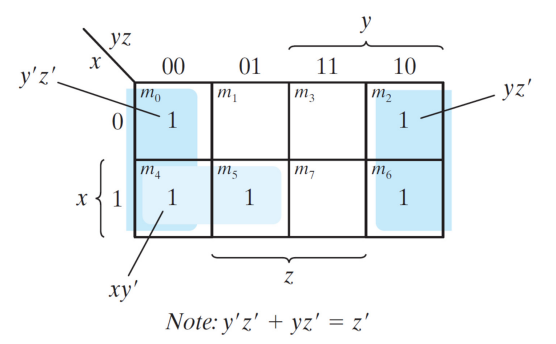
즉 그림 예시의 경우에 4개씩 묶어낼 경우가 없다고 생각하는 것이 아닌
m0 m2 m4 m6을 하나로 묶어낼 수 있는 경우가 있는것이다.
3-3. 4변수 k-map
마지막으로 4변수 k-map이다. (더 많은 변수가 있는 경우도 있지만, 너무 복잡한 경우는 컴퓨터가 처리하기에)
2변수든 3변수든 4변수든 모두 같은 원리의 maping 방식이 적용된다.


따라서 2^n (n = 4 3 2 1 0) 이므로, 16개 8개 4개 2개 1개 의 경우에 따라서 1이 들어간 칸을 묶어낸다.
이후 변하지 않는 변수만 적어주면 완성.
'디지털공학 > Chap 3.' 카테고리의 다른 글
| Chap 3. 게이트 레벨 최소화 (4) . Gate-Level Minimization (0) | 2022.01.13 |
|---|---|
| Chap 3. 게이트 레벨 최소화 (3) . Gate-level minimization (0) | 2022.01.11 |
| Chap 3. 게이트 레벨 최소화 (2) . Gate-level minimization (0) | 2022.01.10 |