3-6. Don't care condition
우리가 앞서 배운 부울함수부터 k-map까지 오면서. 논리의 합은 2진 체계 내에서 1과 0으로 정의되었다.
(어찌됐든 0이나 1로 표현됐다는 것)
이 상황은 함수의 입력 변수 값들의 모든 조합이 유효하다는 가정하에서 이루어졌다.
하지만, 실제로는 어떤 함수에서 입력 변수들의 특정조합이 유효하지 않은 경우 가 있다.
실제로 10진수 4bit 체계의 이진 코드에서는 사용되지 않는 조합이 6가지나 존재한다. (!!)
이렇게 몇 개의 입력 조합에 대해 함수 ㅇ값이 규정되어 있지 않은 경우 이 함수를 incompletely specified function (불완전하게 규정된 함수) 라고 부른다.
따라서 규정되지 않은 최소항들에 대해서 함수 값은 1이되던 0이되던 상관하지 않는다 (don't care)

예제를 보면서 알아가보자.
어플리케이션에서 (선제 조건에서) don't care condition이 있는 경우 d( a b c d )의 형태로 표현한다.
그리고 네모칸 안에는 X 의 형태로 써 넣는다. (0이나 1로 정의되지 않았음)
그렇다면 예제에서 X자가 들어가 있는 변수조합중 하나인 0 1 0 1 이라는 조합이 들어왔다면 결과가 무엇일까???
실제 답은 모른다 이다. 실제 무슨 값이 출력은 되겠지만 해보지 않고서 우리가 예측할 순 없다는 이야기이다.
(예측한 정확한 값이 나와야 하는 기기에서 예측이 안된다면 무슨 소용이지?? 라는 생각이 당연하다)
역설적이게도. 우리는 무슨 값이 나올지 모르기 때문에 저 X자에 0이든 1이든 우리가 원하는 값을 대입할 수 있다.
따라서 예제와 같이 우리가 '주항'을 만들기 더 쉽고 간편하게 묶을 수 있는 방법대로 묶을 수 있게 된다.
결국 0과 1 어느것으로 선택할지 결정되면. 결국 1로 선택하게 된 최소항들의 합으로 표현된다.
3-7. NAND(not and)와 NOR(not or) 구현
기본적인 논리 연산의 게이트는 AND와 OR이고 그리고 이것들로 이루어진다.
그러나 실제 디지털 회로는 AND나 OR보다는 NAND 또는 NOR게이트로 구성되는 방식이 더 많다.
그것은 NAND gate는 universal gate(범용적 gate)로 불리우기 때문이다.
(NAND gate만 가지고서 회로를 꾸밀 수 있다. / 혹은 NOR gate 이용.)
다음 사진은 회로 설계에서 어떤 심볼로 표현되는지 보여준다.

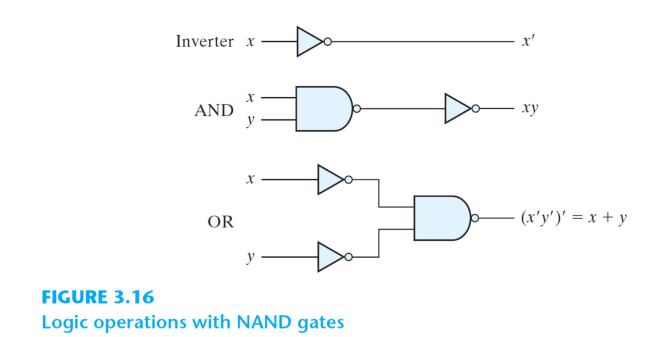
NADN와 NOR은 결국 AND와 OR의 보수형식 (NOT)이라고 생각하면 된다.
부울 함수를 NAND gate 만으로 구현하는 편리한 방법은 부울 연산자 형식으로 간략화된 부울 함수를 구한 후, 그 함수를 NAND 논리로 변환하는 것이다.
위의 그림과 같이 NAND 게이트를 이용하여 AND, OR, NOT의 기능을 모두 수행하게 할 수 있다.
그런데 인버터는 인버터를 사용하지 않고 어떻게 NAND로 구현한다는 말인가?
이것은 Single input NAND gate를 이용하면 가능하다. (이상하다. 인풋은 두개인데 왜 single일까?)
이것은 간단한 사고실험으로 알아볼 수 있다.
- NAND 로 인버터 만들기 -
1. AND의 두 입력이 모두 다 1로 들어왔을 때만 1, 그렇지 못한 경우는 0을 출력한다.
2. NAND는 AND의 보수이므로. 모두 다 1로 들어왔을때만 0, 그렇지 못한 경우는 1을 출력한다.
3. NAND의 한가지 인풋을 0으로 정해둔다면. 다른 한 입력이 무엇이냐에 상관 없이 1을 출력한다.
(0을 가진 조합으로는 01, 00 밖에 없는데. NAND는 이 두 경우 모두 1로 출력하기 때문)
4. NAND의 한가지 인풋을 1로 정해둔다면. 다른 입력이 1인경우 (11)로 0을 출력, 0인경우 (10)으로 1을 출력한다.
(1을 가진 조합에서 11,10의 두 경우가 있는데. 11은 0출력, 10은 1을 출력한다.
이러한 사고실험의 결과를 보았을 때. NAND의 한가지 인풋을 1로 고정시켜 둔다면 인버터와 같은 연산을 하게 된다.
(곧바로 이해가 안가더라도 한번만 곰곰히 생각해 보면서 순서를 따라가면 금방 이해된다.)
'디지털공학 > Chap 3.' 카테고리의 다른 글
| Chap 3. 게이트 레벨 최소화 (4) . Gate-Level Minimization (0) | 2022.01.13 |
|---|---|
| Chap 3. 게이트 레벨 최소화 (2) . Gate-level minimization (0) | 2022.01.10 |
| Chap 3. 게이트 레벨 최소화 (1) . Gate-level minimization (0) | 2022.01.10 |