0.
디지털 시스템에서 논리 회로는 조합 회로(combinational) 이거나 순차(sequential) 회로이다.
논리 회로에서 출력이 현재 입력만의 함수이면 이를 조합 회로라고 한다.
조합 회로는 부울 함수들에 정의된 논리 연산을 수행한다.
이에 반해 순차 회로는 논리 게이트에 저장 회로를 포함한 회로이다.
따라서 순차 회로의 출력은 저장된 값과 입력 값에 따라 변한다.
4장에서는 조합 회로에 대해서 먼저 알아보겠다.
4-1. 조합 회로.

조합 회로는 결국 논리 게이트들의 연결로 이루어진다.
조합 논리 게이트는 입력단의 신호에 의해 출력을 만드는데, 이때 주어진 입력 데이터를 처리하여 내보낸다.
여기서 우리는 주어진 회로의 연산 과정을 분석하거나, 주어진 연산을 하는 조합 회로를 설계할 것이다.
4-2. 분석 과정.
먼저 우리는 주어진 회로가 조합 회로인지, 순차 회로인지부터 판단해야 한다.
이 회로가 조합 회로라는 것을 확신할 수 있는 방법 두가지가 있는데, 그것은 바로 Feedback 회로나, 메모리 소자가 없다는 것이다. (반대로 있으면 순차 회로이다)

위와 같은 회로가 주어졌을 때. 피드백 회로가 없고, 메모리 소자도 없으므로. 조합 회로이다.

1. 먼저 입력 변수와 연결된 게이트의 출력에 임의의 기호를 붙이고, 그 게이트 출력의 부울 함수를 구한다.

2. 구한 함수에 연결된 게이트의 출력에 또 다른 임의의 기호를 붙이고 그 출력의 부울 함수를 구한다.
(회로의 출력을 구할 수 있을 때까지 위의 과정을 반복한다)

3. 앞서 정의된 함수를 반복적으로 대입하여 입력 변수로 표현되는 출력 부울 함수를 구한다.

결국 우리는 위의 방법대로 구해진 부울 함수에 각 변수조합을 대입하여 진리표를 알아낼 수 있다.
이렇게 구해진 부울 함수와 진리표를 토대로 어떻게 동작하는 회로인지 알아낼 수 있다.
(실제 이 예시의 회로는 가산기 회로로 변수 ABC에 대해서 2진 덧셈을 해 주는 역할을 한다.)
4-3. 설계 과정
조합 회로의 설계는 분석 과정의 반대 과정이다.
1. 회로의 설계 사양에서 필요한 입출력의 개수를 구하고, 각각의 입출력에 기호를 지정한다.
2. 입력과 출력 사이에 요구되는 관계를 정의하는 진리표를 구한다.
3. 입력 변수의 함수로서 각 출력에 대한 간략화된 부울 함수를 얻는다.
4. 논리 회로도를 그리고 설계를 검증한다.

위와 같이 BCD 입력에서 3초과 출력 코드로의 변환을 시킬 수 있는 회로를 설계한다고 해 보자.
각 코드는 4개의 비트를 사용하기 때문에 4개의 입력과 4개의 출력이 필요하다.
이때 위의 진리표에서, 4개의 입력 변수를 사용하기 때문에 2^4으로 16가지의 입력 조합이 가능하지만.
10진수 0~9까지만을 나타내는 BCD 코드 10가지 만을 사용하고 나머지 6가지의 조합은 don't care condition이다.
이 값들은 BCD에서 아무런 의미가 없고 또한 무슨 일이 일어나지도 않는다.
그러므로 don't care condition 을 사용하여 간단한 회로를 만들도록 정해주면 된다.
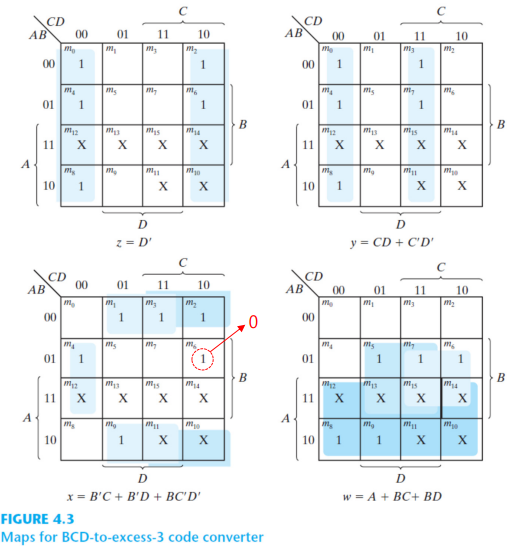
다음으로는 각 출력 변수마다 (z y x w) k-map 을 이용하여 간략화된 부울 함수를 구한다. (don't care은 위치고정)
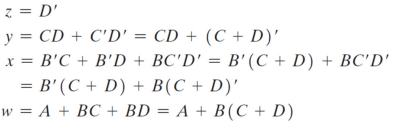
이렇게 구해진 각 변수에 해당하는 부울 함수를 AND와 OR, NOT gate를 이용하여 설계한다.
(회로 설계에 들어가기 전에 각 변수의 결과에서 OR 결합으로 묶어낼 수 있는 항은 묶어서 간략화한다.)
다음은 이렇게 정리된 부울 함수들을 토대로 설계한 논리 회로이다.
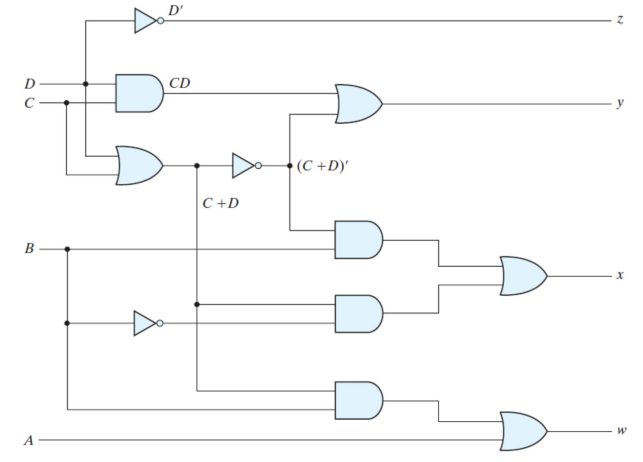
4-4. 2진 가산기 (Half adder / Full adder)
반가산기 (half adder)란 carry를 고려하지 않는 덧셈을 수행한다.
반가산기는 2개의 입력과 2개의 출력을 사용한다.
입력 변수는 각각 가수와 피가수의 bit 입력이고, 출력은 합과 캐리를 만든다.
이때 carry를 의미하는 출력 C는 두 입력이 모두 1일 때만 1이 되고, S의 입력은 bit합의 끝자리 유효숫자를 나타낸다.
즉 각각 두 비트에 대한 덧셈은 수행할 수 있지만, 두 비트를 넘어가는 덧셈은 수행해주지 못한다.
(자릿수가 많은 2진수를 더할 때 사용할 수 없다.)
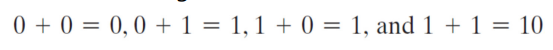
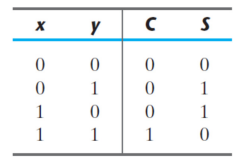
설계 과정을 따라가면, C에 대한 함수와 S에 대한 함수를 k-map으로 만들어 읽고, 그에 대한 부울 함수를 구한다.
이 식에 대한 그대로의 설계를 해보자면.
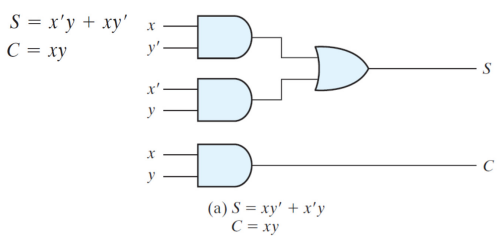
이고, x'y + xy'의 연산은 XOR연산으로 볼 수 있기 때문에
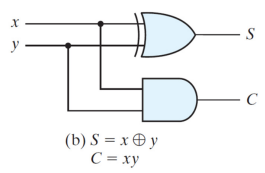
으로 설계될 수 있다.
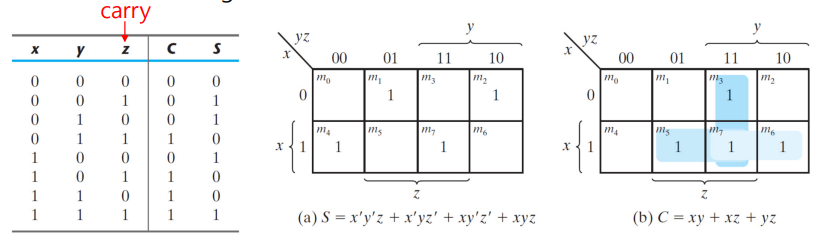
전가산기는 n비트 2진수의 덧셈에서 필요한데, 반가산기와 연산에서 다른 점은. 덧셈 과정에서 최하위 비트부터 시작해서 오른쪽에서 왼쪽으로 같은 자리의 두 비트들을 더하면서 진행된다는 것이다.
(이런 점에서 위의 반가산기와 차이점이 나는 것.)
따라서 carry의 의미를 가지는 입력 하나가 더 필요하기 때문에 3개의 입력단이 필요하다. (실제로는 두 자리 bit 덧셈)
위의 C와 S에 대한 부울 함수를 토대로 회로 설계를 해보면.
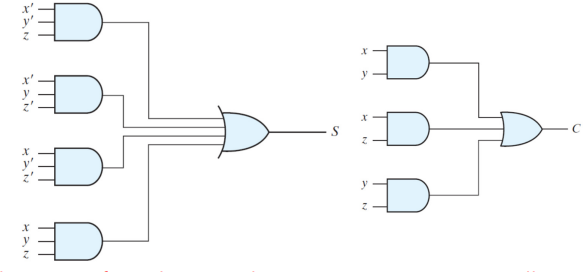
위의 그림과 같고. 이는 곱의 합 형식으로 표현됐는데, 실질적으로 많이 사용하는 형태는 아니다.
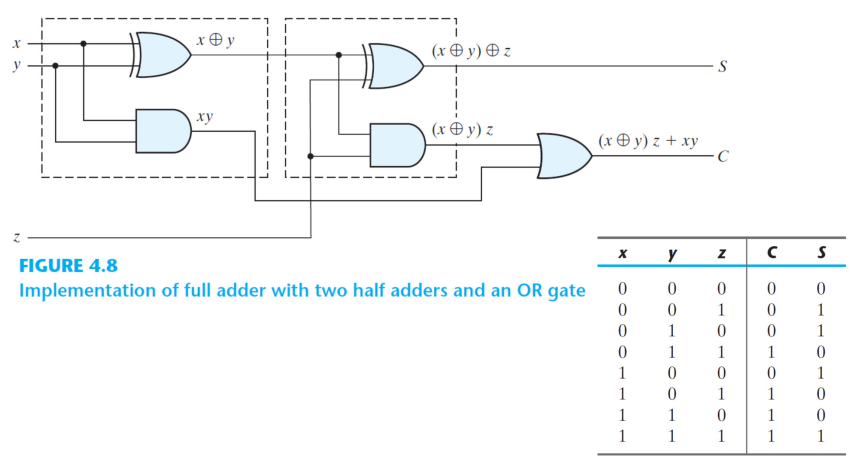
위와 같이 전가산기의 논리회로 구성은 반가산기 두 개의 연산으로 처리될 수 있다. (더 범용적 표현)
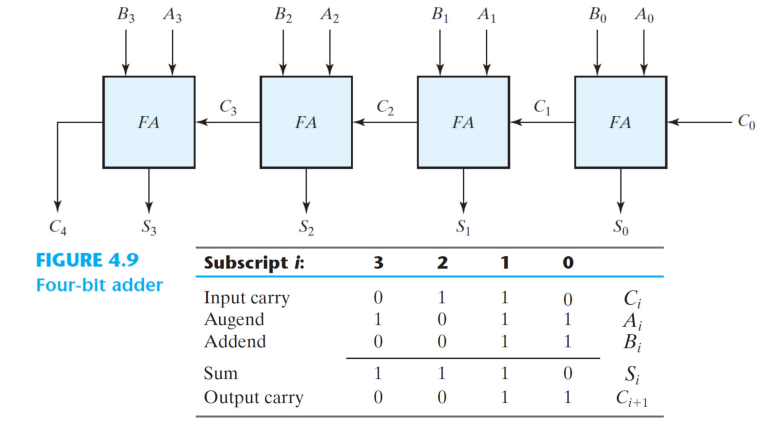
이렇게 이루어진 전가산기를 이용해 2진수의 덧셈을 할 수 있게 됐다.
이런 전가산기들을 여러 개 이어 붙여 다양한 비트수의 계산을 할 수 있게 된다. (그림에서는 4bit)
처음 가산기의 입력 캐리 C0는 0으로 설정되고, C1,2,3,4는 전가산기를 통과하며 캐리를 생성하고 넘겨준다.
위와 같은 4비트 가산기의 처리 과정을 보자면.
A와 B로 대표되는 입력은 모두 동시에 전가산기에 각 들어온다.
맨 오른쪽의 첫 단의 전가산기의 캐리 변수에는 0으로 설정된 값이 들어온다.
C0 + A0 + B0의 값을 연산하고 자릿수에 맞는 부분만 S0로 처리되고, 넘어간 carry가 있다면 c1에 1로 전달한다.
다음 전가산기에서 넘어온 C1 값에 A1+B1을 합해서 연산하고 carry가 있다면 c2로 전달한다.
이런 과정을 거쳐서 각 S3,2,1,0의 값이 생성되고, 만약 마지막 단에서 남은 C4의 carry가 있다면 end carry가 존재한다.
※Carry propagation. : C0 로 들어온 시작 캐리는 최종 캐리인 Ci 까지 전달되어야 하고, 이는 전송되기까지 시간이 걸린다는 뜻이다.
위의 4비트 가산기의 처리 과정을 같이 보았을 때. C0에서 설정된 0이 들어오며 Ai, Bi의 입력값과 연산이 이뤄지고, 그 다음 넘어간 bit의 캐리가 C1에 들어가면서 Ai+1, Bi+1 과 연산이 이뤄진다.
하지만 실제 입력되는 Ai와 Bi 또한 그 다음 입력값들은 동시에 회로로 입력된다.
여기서 위의 회로의 한계점이 생긴다. 결국 C0에서 Ci까지 전달되는 시간이 걸리고, 그 사이에는 안정된 값이 나오지 않거나 불안정하게 존재하게 되는 것이다.
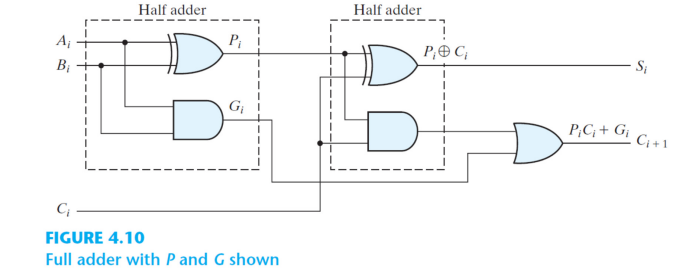
위와 같은 한계점을 극복하기 위해. 시간차를 극복해주는 연산이 P와 G로 극복된다.
위의 연산과정에서. P와 G라는 변수는 A와 B가 주어졌을 때 전가산기 안에서 바로 생성되는 변수이다. (입력단 gate)
입력단 gate에서부터 바로 들어오고 나오는 출력값이기 때문에 Pi값과 Gi값 또한 동시에 주어지는 입력값 A,B에 대하여 즉각적으로 발생된다.
이때 Pi는 전달 캐리라고 하고, 캐리가 i단계에서 i+1의 단계로 전달되는 것을 의미한다.
Gi는 생성 캐리라고 하며 Ai와 Bi가 모두 1일 때는 입력 캐리 Ci와 관계없이 출력 캐리를 만드는 역할을 한다.
이후 각 단계의 캐리 출력에 대한 부울 함수를 쓸 수 있고. 각 Ci의 아랫단의 식을 대입해주면 된다.
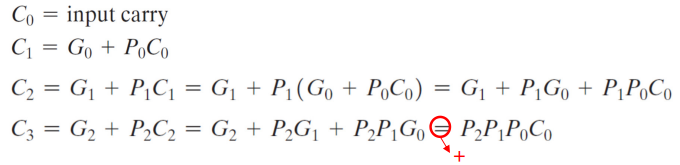
이렇게 동시에 들어온 Ai와 Bi에 대한 변수에서, 캐리 변수가 순차적으로 Pi와 Gi의 합으로써 전달될 수 있다.
이 연산에서 모든 캐리값 Ci값은 모두 C0라는 변수로 표현된다.
C0라는 시작 캐리값은 특정 값으로 고정된 값이기 때문에. 순차적으로 진행되고 있더라도, 모든 가산기의 캐리값이 즉각적으로 발생된다. (P와 G가 gate에서 입력값을 받아 즉각 생성되고, C0라는 고정된 값과 연산만 해 주면 되기 때문)
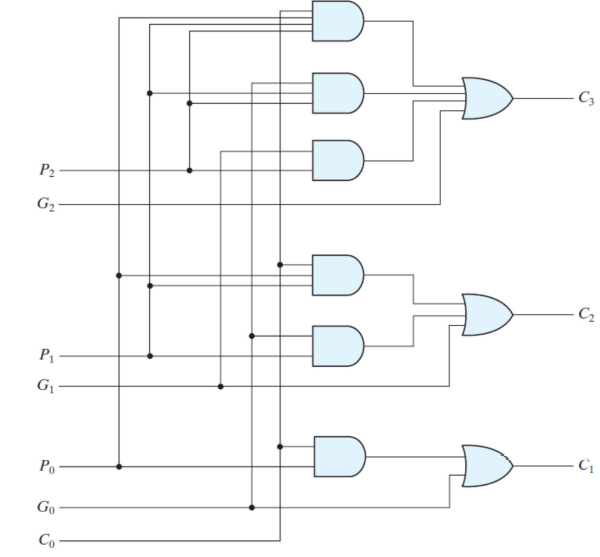
이러한 과정을 가진 논리 회로도를 캐리 룩어헤드 생성기라고 하고 다음과 같이 구성된다.
이러한 과정을 거치면서 위에서 언급한 한계점인 순차적 연산 진행을 가능하게 한다.
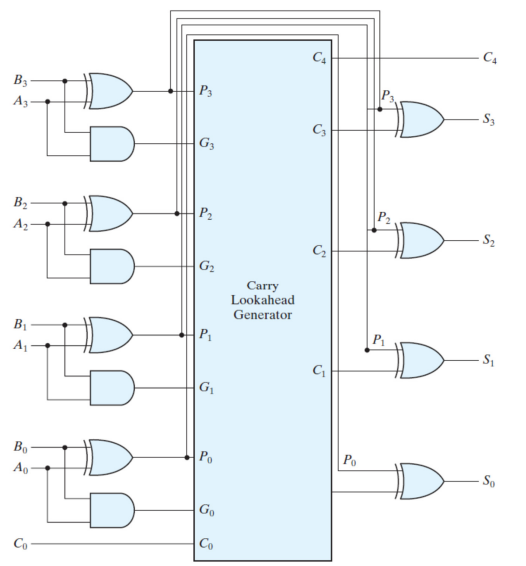
이렇게 캐리 룩어헤드 생성기의 회로를 거치는 4비트 가산기는
'디지털공학 > Chap 4.' 카테고리의 다른 글
| Chap 4. 조합 논리 (2) . Combinational Logic (0) | 2022.01.14 |
|---|