<Diode-Connected Load의 특성 및 Output Resistance>
앞서서 Resistive load를 살펴보았다.
그러나 CMOS 공정에서 정확한 값을 가지는 resister를 구현하는 것은 어려운 일이다.
(PVT variation)
따라서 Rd를 통해 동작하는 CS Stage에 경우에는
부정확한 Rd 값으로 인해 Gain이 각 stage마다 모두 다른 경우가 발생하게 된다.
이러한 PVT variation의 효과를 없애기 위한 대안으로
Diode Connected MOS를 load에 사용하는 방법이 있다.

M2의 트랜지스터 형태처럼 Gate와 Drain의 potential을 공유하도록 만들어 놓은 구조가 Diode connected다.
Diode connected MOS는 gate와 drain이 같은 voltage potential을 공유하기 때문에
동작 조건 Vds > Vgs - Vth에 의해
항상 saturation region에서 동작하는 것을 알 수 있다. (MOS가 on인 경우에)



이때 Diode connected MOS에서 구한 output impedance 값은
loosely하게 판단했을 때
다른 MOS의 source에서 보이는 impedance 값과 같다고 생각할 수 있다.
<Voltage Gain 및 특징>

diode connected MOS를 load로 가지고 있는 CS stage의 Gain을 구해보면

으로 수해볼 수 있고 이를 다시 풀어서 정리해보면


즉 같은 공정 parameter를 가지고 있는 MOS라고 하였을 때.
Gain이 각 소자의 dimention 비의 루트 형태임을 알 수 있다.
더하여 body effect까지 무시한다면 (η = 0)
전체 stage의 gain은 단순한 dimension 비의 루트 임을 알 수 있다.
중요한 포인트는
1. M1, M2는 모두 동일한 PVT variation 영향을 받는다.
voltage gain 수식에서.
PVT variation의 영향을 받아도
서로 분자 분모에 영향을 주어
PVT variation 영향 요소를
서로 cancle-out 해줄 수 있다.
2. input-output characteristics는 상대적으로 Linear 하다.
resistive load의 경우를 보았을 때
Vin에 따라서 gm이 변하고
나아가 voltage gain이 변하게 되는 nonlinear 특성이 존재했다.
그러나 Diode connected load를 사용하는 경우
input voltage swing의 크기에 상관없이
상대적으로 더 Gain이 Linear하게 나타나는 특징을 가지고 있다.
(body effect가 없다고 가정할 때)
즉, 이러한 형태는 PVT variation 효과로부터
상대적으로 훨씬 영향을 받지 않고
linear한 voltage gain을 갖는다는 장점이 있다.
<CS stage Diode connected load의 특징 1>
input/output relationship
Diode connected load 를 가지는 stage의 특성을 수식으로 알아보자.

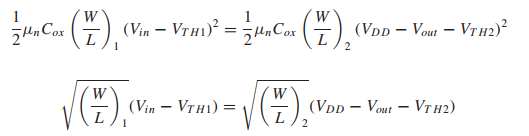
M1 에서 Vin에 의해 drain current가 형성된다.
이 current는 M2의 darin current로 공유된다.
이때 M1이 발생시킨 Id는 M2에 외부 압력으로 작용한다.
만약 Id의 값이 증가한다면
M2의 MOS는 증가된 Id의 값을 충족시키기 위해 Vgs potential이 증가하면서 Id를 "따라간다"
즉, 다시말하면 Id 값을 M2의 입장에서
"입력"으로 사용했고
Vgs로 "출력" 됐다고 생각할 수 있다.
< CS stage Diode connected load의 특징 2>
동일한 drain current에 의한 현상
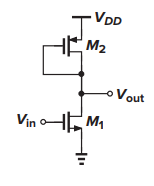
load에 PMOS를 사용하는 경우도 생각해 볼 수 있다.
어떻게 생각하면 큰 Gain을 얻기 위해
PMOS를 사용하는 것이 더 좋을 수 있다.
(why?) 다시한번 이 stage의 gain을 살펴본다면 다음과 같다.
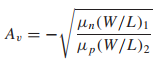
이때 mobility 가 hole이 electron에 비해 0.5배의 값을 가지고 있기 때문이다.
(분모가 작아진다)
따라서 PMOS를 사용할 때가 NMOS를 사용할 때 보다 더 높은 Gain을 얻을 수 있다.
이때 M1과 M2 트랜지스터의 Id current가 동일하다는 조건을 생각해 보았을 때.
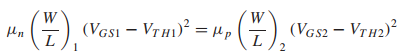
위의 수식이 성립하게 된다.
또한 같은 조건 하에서
Gain과 gm의 특성을 살펴볼 수 있다.
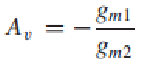
body effect가 없다고 가정할 때
stage의 Gain은 위와 같이 표현할 수 있다.
이때 drain current 값이 일정할 때.
gm과의 관계식은 chap 2.에서 보았듯이 다음과 같다.
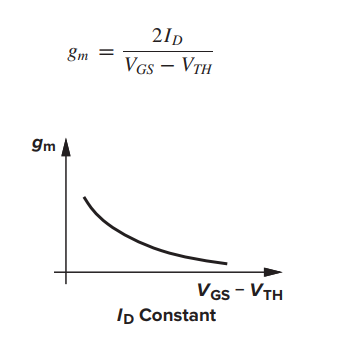
지금 우리가 살펴보고 있는 stage의 M1, M2에 흐르는 Id는 동일하다.
이 조건에서
M1, M2의 Vgs1, Vgs2의 비율은 항상 동일하다.
이것을 Gain 수식에 대입하면
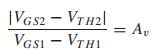
이때 앞서 구했던
dimention의 비율로 나타났던 gain 수식과 비교해볼 수 있다.
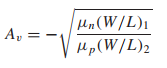
정리하자면.
M1과 M2의 voltage Gain을 조절하기 위해서
Demestion을 조절할 수 있다.
이에 따라 소자가 Id current를 drive할 수 있는 strength가 달라지게 된다.
이때 M1, M2에 흐르는 Id current는 동일하기 때문에
결국 M1, M2 트랜지스터의 Vov값을 조절해 주어야 하는 결과를 낳는다.
즉
높은 voltage gain을 위해
M2의 dimension을 낮추었다고 했을 때.
M2가 Id를 drive 할 수 있는 Strength가 약해져
Vov의 값이 그 약해진 만큼을 보상하기 위해 값이 상승한다.
이렇게 되면 Vout node에서의 output swing 범위를 제한한다. (trade off)
'Circuit > Analog' 카테고리의 다른 글
| 3-1) Common Source stage with Resistive load (0) | 2024.09.04 |
|---|---|
| 3-0) Single Stage AMP (0) | 2024.09.04 |
| 2-2) MOSFET Structure and Symbols (0) | 2024.09.04 |
| 2-1) MOSFET as a Switch (0) | 2024.09.04 |