- Channel Charge Density

앞선 포스트에서도 다뤘던 부분이지만 다시한번 짚고 넘어가면서 이해해보자.
단위 length당 W만큼의 부피에서 차지하는 Charge의 Density를 정량적 수치로 구하는 과정이다.

위에 표시된 식에서 보자면. 단위 Length당 W의 부피이므로 그 요소인 Length는 1로 분모에, 분자의 그 Charge의 양은 해당 W폭에 포함된 Charge의 양을 구해내면 되므로.
Charge의 양을 구하기 위해 Cox로 표기된 산화물 (절연체 Insulator)이 가지는 Capacitance 양
(-> Gate와 Body에 작용되는 전기장 세기)
또한 문턱전압 Vth보다 얼마나 강한 전압이 걸렸는지에 따라 Channel의 두께가 결정되므로 Vgs - Vth의 값을 곱한다.
* 이때 Vgs - Vth는 Overdrive Voltage라고 부르기도 한다.

앞에서 알아보았듯이. Source와 Drain이 Gate와의 전위차가 서로 상이하기 때문에 Channel이 특정 지점에서 (그림상에서 x축의 시점에서) 서로 다른 두께를 가지므로 Charge Density 또한 다르게 나타나야 한다.
그것을 일반화 하여 특정 지점 x에 대해서 작용되는 Overdrive Voltage를 일반화 하여 적용된 식이 위의 식이다.
- Charge Density와 Current

위에서 구해낸 Q의 값을 가지고 우리는 Channel에 통하는 전류량을 구해낼 수 있다.

이때 Charge density인 Q와 해당 전자의 속도의 정의를 가지고 식을 정리하면 위와 같은 식을 얻어낼 수 있다.
( Q = 길이당 차지하는 Charge q , v = 시간당 이동한 거리 Length)

기본 정의에 의해 정리가 됐다면. 전자의 입장에서 바라본 정의로써 접근하면 된다.
I = Qv에서, v로 표현된 전자 혹은 정공의 속도는 전기장 내에서 mobility 값인 μ로 표현되고, dV/dx = E의 전기장 표현으로 바꾸어 쓸 수 있다.
따라서 특정 x위치에서의 Charge Density의 식을 가져와 서로 곱해주면 위의 두번재 식과 같이 Id를 표현할 수 있다.

이때 총 Channel 내에서 흐르는 전류량을 구하기 위해서 특정 위치 x가 아닌 0~L 까지의 값으로 적분을 해주면 총 채널길이 L 내의 Current양을 구해낼 수 있게 된다. (1번식)
그렇게 정리된 마지막 줄의 Id식으로써 MOSFET Channel 내에 흐르는 총 전류량 Id를 계산할 수 있게 됐다.
*식이 정리됨으로 모빌리티, Cox, Channel의 W/L, Vgs, Vth, Vds가 모두 MOSFET 전류의 요인이라는 것을 알게 됐다.
- Drain 전류와 Vds/Vg의 관계

위의 그래프는 우리가 구해낸 Id의 전류 식에서 최대값을 갖는 지점을 찾아낸 것이다. (수학적으로는 미분으로 극값)
(구해진 값은 위의 Y축 옆에 써있는 값)

위에서 알아본 식에서 Vds의 값을 변수로 두고 Vg의 값을 고정해둔 상수값이라고 생각했을 때 Id의 전류값은 Vds의 값이 Vgs-Vth의 값. 즉 Gate와 Source간의 전위차에서 문턱전압 Vth를 뺀 값이 Drain - Source 간의 전위차와 동일해질 때 최대의 전류값을 갖는다.

위의 그래프는 상수로 고정시킨 값인 Vg의 전압을 차례로 변화시킬 때의 Id의 그래프이다.
이때 위에서 알아본 Id전류 최대값의 점만 찍어서 확인해볼 때 이는 2차 그래프와 유사하게 그려진다.
또한 Id의 값은 Vgs-Vth의 값이 Vds와 같아질 때 최대로 흘렀으므로. Id의 최댓값은 (Vgs-Vth)^2의 값에 비례한다.
* 이렇게 알아낸 Id의 수식에서부터 Vds의 변수에서는 Id의 최대값을 가지는 지점을 찾아냈고, Vg의 변수에 대해서는 제곱의 형태로 (2차식의 형태로) 비례하여 나타난다는 것을 알 수 있었다.

이렇게 Vds나 Vg의 변수에 대해서 변화할 때에는 Id의 값이 2차식의 형태로 진행되었다.
그러나 이 때 Vds가 아주 작은 영역. 즉 Drain-Source간의 전위차가 매우 작은 영역에서 MOSFET이 ON되었을 때는 1차식과 같은 Linear한 형태로 나타난다. (여기서도 Vgs의 전위차가 클수록 더 급한 기울기를 가진다)
I-V의 관계에서 기울기가 1차식으로 나타났다는 것은. 위의 그림에 있는 수식처럼, 옴의 법칙 V=IR에 의해 Vgs-Vth등 기타 요인에 의해 Linear한 변화를 하는 저항의 값을 나타낸다는 걸 알 수 있다.
*Vds가 매우 작은 값인 영역에서 동작시키려는 의도는 MOSFET을 Switch로 사용하려고 하기 때문이다.
우리가 흔히 사용하는 Switch는 양단이 떨어져 Off되어 있는 상태에서는 전류가 흐르지 않는 상태, 즉 저항이 무한인 상태이고, 양단을 쇼트시켜 On시킨 상태에서는 떨어져있던 양단의 전압이 같아지면서 전류를 흐르게 한다.
이렇게 사용되는 MOSFET은 Vds가 매우 작은 영역에서 빠른 속도로 동작하므로, 저항과 같은 동작을 하게 된다.
- Different Regions of Operation
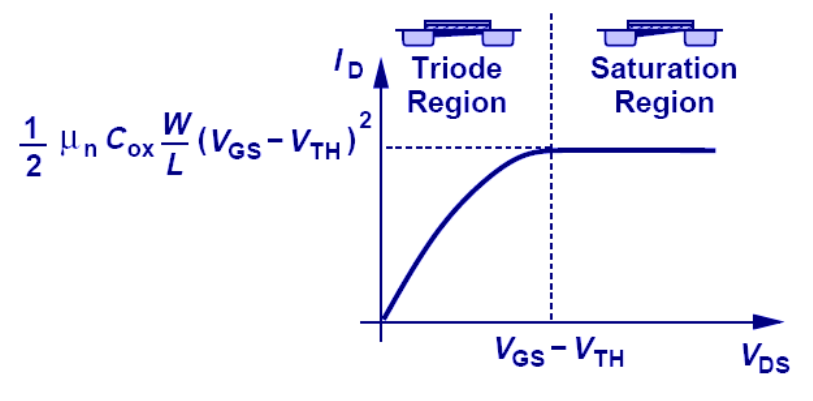
이렇게 MOSFET은 Triode 영역과 Saturation 영역으로 나뉘어 동작하게 된다.
Triode 영역은 위에서 알아본 것과 같이 Switch의 동작을 할 때 R의 저항처럼 Linear하게 동작하는 영역이다.
Saturation 영역은 Vds > Vgs-Vth인 지점. 즉 MOSFET channel이 Pinch off되는 지점부터는 Vds는 더이상 Id에 영향을 주지 못하면서 Vg에 의해서만 Id의 값이 변하는 영역이다.
*Channel 이 끊어지기 때문.
Saturation 영역에서 Current Source로 사용될 수 있는 이유도. Pinch off에 의해 Vds의 값이 얼마나 더 증가하던 ideal 한 Current Source로써 우리가 의도한 전류가 일정하게 유지되기 때문이다.

따라서 동작영역을 수식적으로 기준을 나눌 수 있다.
Linear : Vds < Vgs-Vth
Saturation : Vds > Vgs-Vth
- Channel-Length Modulation / 변수 λ

앞서 배운 수식에서는 Saturation 영역에서는 정확히 Vgs-Vth의 값이 Vds의 값으로 걸렸을 때 최대의 전류값 Id로 일정하게 흐른다고 생각했지만. 실제 동작에서는 Vds의 값이 Saturation 영역 내에서 점점 증가할 때 λ라는 값의 영향을 받으며 조금씩 Id의 값이 Vds의 증가에 따라가는 모습을 보인다.

이 때 λ의 변수는 MOSFET의 channel 길이의 변화에 관계가 있다.
실제 소자값의 측정에서. A/R 값이 같으면 전류식 Id에 의해 같은 수준에서 Saturation current가 형성되어야 하지만. Channel 길이가 짧은 소자일수록 Vds의 증가에 따라 Channel Modulation 수치가 커진다.
반대로 같은 A/R값을 가진 소자일지라도 Channel의 길이가 상대적으로 긴 소자일수록 Channel Moduration 수치는 작아진다. (Current source 혹은 AMP로 사용하기에는 Channel 길이가 더 긴 것이 적합하다는 것을, 반대로 S/W동작으로는 길이가 더 짧은 것이 적합하다는 것을 알 수 있다.)
- Transconductance - dId/dVgs



MOSFET의 Transconductance는 gm이라는 변수로 취급된다.
gm의 의미는 드레인 전류 Id의 값이 Vgs의 변화에 따라 얼만큼의 변화량을 갖는지 나타내는 척도이다.
변화량을 알아보기 위해 Id의 값에서 Vgs에 대한 미분을 진행하고, 그것의 식을 조작하면서 여러가지 수식으로 나타낼 수 있다.
1. W/L = constant / Vgs-Vth = variable (첫번째 수식)
gm ∝ √Id , gm ∝ Vgs-Vth
2. W/L = variable / Vgs-Vth = constant (두번째 수식)
gm ∝ Id , gm ∝ W/L
3. W/L = variable / Id = constant (세번째 수식)
gm ∝ √(W/L) , gm ∝ 1/(Vgs-Vth)
'반도체 소자, 회로설계 > MOSFET' 카테고리의 다른 글
| MOS 와 MOSFET (4) - Large / Small-Signal Models, PMOS tr. (1) | 2022.03.30 |
|---|---|
| MOS 와 MOSFET (3) - gm의 조작 / Velocity Saturation / Body Effect (0) | 2022.03.29 |
| MOS 와 MOSFET (1) - 정성적 이해 (0) | 2022.03.16 |