- Doubling of gm Due to Doubling W/L
저번 포스트에서 알아봤던 Transconductance 값인 gm은 Gate의 전압이 변함에 따라 Vd가 바뀌는 정도를 나타낸다.
이 gm의 값이 크면 클수록 Amp로써의 증폭률도 커지는 것이기 때문에, 높은 gm의 값은 Amp로써 동작시키기에 좋은 소자로 볼 수 있다. 따라서 각 변수에 따른 gm의 비례값을 이용해 늘리는 방법을 보자면.


왼쪽부터 W/L , Vov, Id값이 상수로 취급되어질 때 다른 변수들로 나타난 gm의 값이다.
왼쪽의 두가지 수식만 보고 소자의 Amp로써의 특성을 인 gm값을 증폭시키기 위해 조작가능한 변수 Vov값과 Id에 관해서 보았을 때. 왼쪽의 수식은 Id에 대해서 gm이 루트값 만큼 비례하고, 우측 수식은 gm의 값이 Id에 정비례한다.
이 결론으로 W/L을 변화시켜 gm을 조절시키는 것이, Vov값을 변화시키는 것 보다 더 효과적이라는 것이다.
(단, 전류 자체도 더 많이 사용하게 된다. 설계자가 원하는 조건을 만들기 위해 변수를 조작하는 것은, 이러한 특성을 이해하고 설계자가 선택해서 설계해야 한다.)

이러한 결론을 통해 단순히 MOSFET 소자 자체의 Channel Width를 두배를 늘리면 gm또한 두배로 늘어난다는 것을 알 수 있는데, 이는 우리가 실제 소자의 Width를 두배로 만들어 gm을 증가시킬 수도 있겠지만, 이미 있는 소자 두개의 Gate와 D/S 자체를 공유시키면서 Width가 증가된 효과를 만들어낼 수 있다.
- Velocity Saturation
Charge가 이동하는 경우는 drift와 diffusion에 의해서 이루어 진다.
* diffusion은 PN접합의 관계에서 서로의 Major Carrier인 hole과 electrion이 다른 밀도의 값만큼 가지고 있는 상태로 접합되어 밀도차에 의해 확산되어 움직이는 것이다. 이 때 Depletion 영역 역시 생성되게 되는 것이고, 이 원리를 이용해서 순방향 전압만 전류를 흐르게 하는 다이오드의 특성을 띄게 된다.
이때 MOSFET에서는 전압에 의한 전기장의 생성, 그리고 그 전기장에 의해 Charge가 이동하므로 Drift에 의한 이동을 하게 되는데, 이때 Charge의 이동 속도에 관한 변수를 이용해 Id의 전류값을 Id = v * Q로 얻어낼 수 있었다.
이 식에서부터 υ = μE (μ : 모빌리티) 라는 속도에 관한 변수를 파악할 수 있게 되었다.

우리는 Current Saturation에서도 보았듯이. 실제 소자의 동작은 어느 일정 수준을 넘어설 때 Linear 한 관계에서 Saturation 영역으로 넘어가 다르게 동작한다는 것을 알고 있다.
이는 우리는 앞에서 정성적으로 파악할 때 Pinch-OFF 라는 Channel이 끊어진다는 것과 PN Junction에서 Depletion 영역 관점에서 생각했다면, 이번엔 Charge의 움직임 변수로 설명할 수 있게 된다.
υ = μE (μ : 모빌리티)
라는 식 또한 재료의 특성에 따라 달라지는 모빌리티의 값이 고정되있는 상태에서는 1차식의 Linear한 특성을 가지지만, 실제 동작은 위의 그래프처럼 일정 수준의 E에서 Saturation이 되는것을 볼 수 있다.
이렇게 Saturation이 되는 이유는 Charge가 이동하면서 Doping Ion들과 충돌하는 Dopant Ion Scattering 이라는 효과 때문인데, Drian 전압이 증가하면서 전계의 세기가 세져 Charge가 더 빠르게 이동하려는 경향과 Charge가 이동하면서 ion들과 충돌하는 세기, 속도가 동일하게 증가하면서 서로의 효과를 상쇄시켜 일정 속도에 이르게 하는 것이다.
*빗방울이 공기 내에서 낙하할 때 일정수준의 속도에 다다르면 더이상 속도가 저항에 의해 평행속도가 유지되는 것과 비슷하다고 생각할 수 있다.

이러한 효과를 알고 나서 다시 Id에 관한 식을 보았을 때. MOSFET에 걸리는 Q를 Gate와 Oxide의 넓이, Cap의 관계 식으로 고치고, 그 식을 미분하여 변화량을 관찰하는 gm의 값으로 변화시킨다면 위의 식과 같은 결론을 내릴 수 있다.
(이 모든 과정은 Linear 구역이 아닌, 포화영역에서의 동작식이다)
이 수식의 해석의 결과 또한 Current Saturation의 해석을 가능하게 한다. (gm 변화량이 일정)
- Body Effect

우리가 기본적으로 MOSFET을 다룰 때 Gate, Source, Drain의 세 단자의 전압값을 가지고 계산하고, 사용하는 것 같지만 사실상 MOSFET은 위의 세가지 단자에 Substrate를 Body라고 칭하며 Body를 포함해 총 4단자 소자로 사용된다.
이때 Body와 PN Junction을 이루고 있는 Source/Drain은 그 Junction 사이에 Depletion 영역이 존재하고. S/D 단자에서 Body쪽으로는 항상 B Reverse Bias되어있는 상태를 유지시키기 위해 접지를 시켜놓아 별로 Body에 대해서 고려를 하지 않았었다.
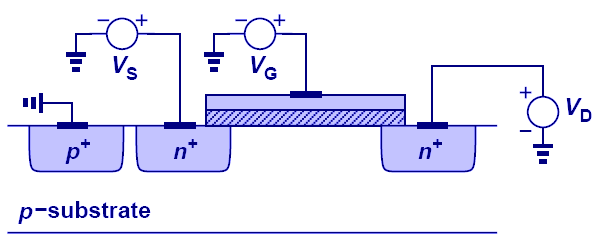
그러나 위의 그림과 같이 Source와 Body는 항상 접지되어 있는 상태에서만 동작하는 것이 아니다. 결국 Source에도 일정 수준의 전압이 인가될 수 있는데, 이 때 Drain 쪽에서 전압이 걸릴때와 마찬가지로 Vds, Vgs의 전위차 감소, PN Junction 관계에서의 Reverse Bias 인가된 조건이 발생되면서 Vth인 문턱전압이 높아지는 효과가 발생하게 된다.
(혹은 body에 - 전압이 인가되어 Vsb >0 인 조건을 만족시켜도 동일하게 Vth가 증가한다.)

위의 식은 Vth가 Vsb Reverse Bias 효과에 의해서 증가하는 관계를 보인 것이다.
Vth0의 초기 문턱전압이 Vsb의 전위차가 0인 관계에서는 Vth가 변하지 않는다는 것을 보여주고 있다.
그러나 Vsb가 0보다 커지는 Vsb>0 즉 역방향 전압이 걸리는 상황에서는 Vth가 점점 높아지는 효과를 보여주고 있다.
(ρ : coefficient, Φ : 도핑에 대한 일함수-> fermi level 관련)
만약 Source에는 접지가 되어있지만, Body에 (-)의 Reverse Bias가 걸렸을 경우는
1) 기판의 (-)전압으로 hole들이 몰려들게 된다.
2) hole의 밀도가 기판의 아랫부분에 밀집 된다.
3) n-channel의 전자 밀집도는 더욱 높아진다.
4) 양쪽의 source와 drain의 junction이 역 바이어스 되어 depletion의 영역이 넓어진다.
5) 소스 단자에는 0V가 인가되어 source와 기판과의 전압차는 drain과 기판보다 작기 때문에 source 쪽의 depletion의 두께는 작다.
6) drain 쪽의 depletion 두께는 두껍다.
7) Channel이 더 몰려든 Electron에 의해 두꺼워진 효과가 있지만 Drain단자의 Depletion 영역의 확대에 의한 Vth 증가가 발생한다.
'반도체 소자, 회로설계 > MOSFET' 카테고리의 다른 글
| MOS 와 MOSFET (4) - Large / Small-Signal Models, PMOS tr. (1) | 2022.03.30 |
|---|---|
| MOS 와 MOSFET (2) - 정량적 이해 (5) | 2022.03.23 |
| MOS 와 MOSFET (1) - 정성적 이해 (0) | 2022.03.16 |